| 日付 | 競馬場 | R | 馬券種 | 組番 | 払戻金額 |
| 12/01 | 中山 | 01 | 単勝 | 10 | 11,520円 |
| 12/01 | 中京 | 03 | 複勝 | 14 | 9,230円 |
| 12/01 | 中京 | 03 | ワイド | 02 – 11 | 8,430円 |
| 12/01 | 中京 | 03 | ワイド | 02 – 14 | 10,080円 |
| 12/01 | 阪神 | 03 | 単勝 | 08 | 8,800円 |
| 12/01 | 中京 | 05 | ワイド | 13 – 15 | 13,350円 |
| 12/01 | 阪神 | 06 | 枠連 | 06 – 06 | 12,900円 |
| 12/01 | 阪神 | 06 | ワイド | 11 – 12 | 12,750円 |
| 12/01 | 中京 | 07 | 単勝 | 03 | 11,800円 |
| 12/01 | 中京 | 07 | 複勝 | 03 | 18,300円 |
| 12/01 | 中京 | 07 | ワイド | 03 – 07 | 10,680円 |
| 12/01 | 中京 | 08 | ワイド | 02 – 05 | 18,550円 |
| 12/01 | 中山 | 10 | ワイド | 05 – 12 | 21,000円 |
| 12/01 | 中京 | 10 | 枠連 | 02 – 07 | 15,770円 |
| 12/02 | 中京 | 05 | 複勝 | 16 | 21,280円 |
| 12/02 | 中京 | 05 | ワイド | 15 – 16 | 21,210円 |
| 12/02 | 中山 | 07 | ワイド | 11 – 13 | 21,000円 |
| 12/02 | 阪神 | 07 | ワイド | 05 – 06 | 23,280円 |
| 12/02 | 中山 | 08 | ワイド | 04 – 11 | 18,480円 |
| 12/02 | 中京 | 12 | ワイド | 07 – 13 | 15,340円 |
期間 12/1-12/2
今週の購入金額 247,800円
今週の払戻金額 303,750円
今週の収支 55,950円
今週単利回収率 122%
累計複利回収率 60%
バンクロール(通帳ベース) 301,340円
というわけで、這々の体で30万円まで回復したのが現在のステータスになります。
ここまでの総購入金額は約400万円で、20万負けなので、一般的な回収率だと95%くらいか。少しずつ取り返していきましょうね。
ようやく溜め込んでたブログの更新が終わったので、今私がやっているチューニングについて説明しましょうか。
的中率5% 回収率150%よりも的中率30% 回収率110%の方が遥かに優秀な馬券師なんだよな。俺の言ってることわかる?
— オイルパラダイス京都 (@oiparasan) 2018年11月29日
結構沢山の人が理解しているようで、そのわりには、ここを最適化しようという議論が皆無に等しいんですよね。
蛇足ではありますが、この1ツイートの仮定のみではどちらが優れているかを一概には判断出来ないとは思います。馬券界の常識が暗黙に仮定されています。その仮定が何か、わかるかな?
私がここ最近チューニングと呼んでいるものもここの最適化で、私が目的としている「収支の最大化」を実現する為に、最も良い的中率と回収率のバランス(正確に言うと、購入金額とのバランス、収支の分散とのバランスも)の馬券購入方法を求めようとしています。
この手の問題を単純にした例題を1つ挙げましょう。
あなたは有料予想家で、今の販売価格は1000円で、1ヶ月あたり100人の購入者がいるとします。売上高は1000円 * 100人 = 10万円/月で、その他経費などはかからないものとします。
有料予想の価格を50円上げると、購入者が1人減るということがわかっています。この時、売上高を最大化する為の価格設定はいくらでしょう。
この問題、解けますか?数学的に解けないとしたら、売上高が最大になる価格設定はだいたいどれくらいだと思いますか?広告の下に解答を書きました。
答えは、販売価格3000円とした時に、売上は最大値18万円を取ります。
売上高をyとすると、yの式は以下のようになります。
y = (1000 + 50x) * (100 – x) ・・・➀
販売価格が1000円の時はx=0を代入すると、1000 * 100になって現在の売上高10万円が出てきますね。
この式を展開すると
y = -50x^2 + 4000x + 100000
平方完成を行うと
y = -50(x – 40)^2 + 180000となり、売上高の二次関数のグラフは以下の通りになります。
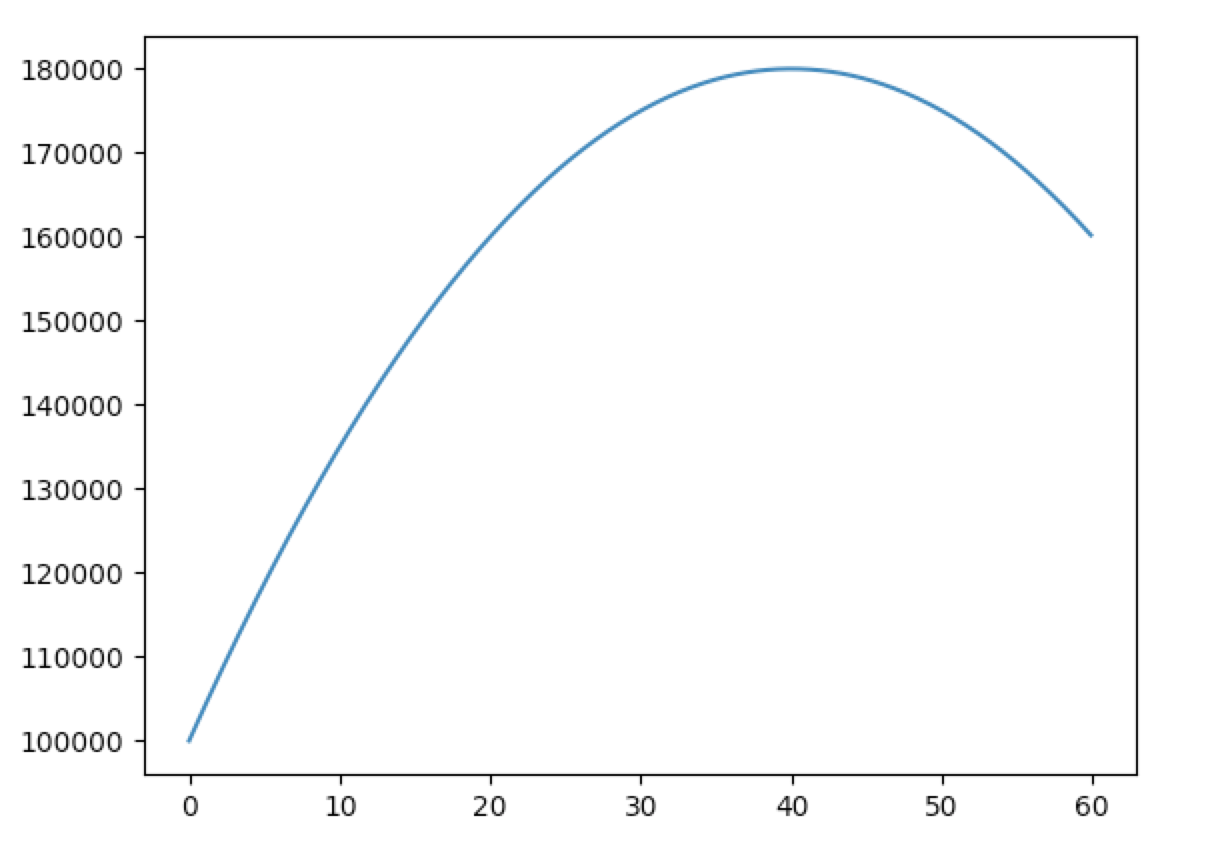
x = 40、つまり販売価格3000円の時に売上高のグラフも頂点の18万円を取っていることがわかります。
まぁ、微分したらx = 40の時にy’ = 0になるので、暗算でも解ける問題です。
x = 39の時は、➀の式はy = (1000 + 1950) * (100 – 39)となりy=179,950円、
おなじくx = 41のときはy = (1000 + 2050) * ( 100 – 41)となりy = 179,950円が求められます。
私がやろうとしていることは、基本的にはこれの発展した微分問題なんですが、複利で運用する前提であったり、上記例題のほど販売価額と購入者の関係がシンプルに線形でなかったり、変数が増えたりするのでいくらか複雑になります。
でも、金融工学の世界ではそれほど難しい問題ではないと思います。
それにどうしてこれほど手間取っているかというと、最終オッズと確定オッズの変動という未知の変数があるからです。
この例題に沿って言うなら、「3000円で売っても、手数料やら税金やら諸々引かれて手取りが目減りする、いくら目減りするかは確率的」というような状況ですね。それゆえに、購入時にリスクの計算が正確に出来ずに困っています。
近年この未知の変数の変化が辛くなってきて、特に的中馬券の確定オッズをOt、最終オッズをO(t-1)としたとき、Ot-1からOtの変化がブラウン運動ではないということは確認しました。
的中馬券の、最終から確定までのオッズの変化はランダムではなく、的中馬券はオッズが下がる確率が高い。
言葉を変えると、最終オッズ提示後から締切までに購入される馬券は、最終オッズ提示までに購入された馬券よりも的中を言い当てているものの割合が高いということです。
なので、的中した際にある程度オッズが下がることは前提として、そのうえで今提示されているこのオッズで馬券を買うべきなのか、というチューニングをしているわけです。
最大効率を犠牲にして、見積もるリスクに大きめのバッファを持たせているのが今の雑なチューニングで、この前挑戦したのは最大効率を狙うチューニングでしたが、少し見積もりが甘くなった可能性はあるかもしれません。
前時代の「優れた商人」の商才とは、感覚的な才覚が数学的な解に漸近できる、という事だと思います。なんとなくで、販売価格が3000円に近い値が出せた。
優れたギャンブラーの博才も同じでしょう。ここで幾ら張るべきかの感覚が、数学的、科学的な正解に漸近できる。しかしそれは科学を超えるものではないんですよね。
Technology will always win.
科学技術は常に勝利をもたらす。
私はそれを信じています。