競馬と私のギャンブル観の話を連載しようと思う。真面目な話をするつもりだ。
その前に3つ、ことわらなきゃいけないことがある。
1つめ、私は競馬は”楽しく負けるべき”だと考えている。
たとえばあなたがカラオケに行ったとして、何時間か歌を歌って、メロンソーダを3杯くらい飲んで、お会計に2,000円くらい支払ったとして、それを「2,000円負けた」とは思わないと思う。
競馬もそれくらいのものであるべきだ。
2つめ、私はまだ競馬で勝てていると宣言出来ないから、こと競馬に関して偉そうなことを言う資格はない。
これから書こうと思っている話は、全て私の戯言と取って頂いて構わない。
勝てる目処はついているので、いつかそれを証明しようとは思ってる。
3つめ、具体的で直接的な手法には言及しない。
多くの人はせっかちだから、明日から使える具体的な方法を求めたがる。
「どういう馬を買えば勝てるんですか」みたいな質問は多い。
でも、必勝法はそういう直接的な施策ではないんだよ。
真の必勝法があるとしたら、いつだってそれは姿勢であり、心構えであり、あり方なんだよ。
以上。
自己紹介をしていないかもしれないけれど、私はパチンコ・パチスロ、麻雀・ポーカー、株のデイトレードまで、多くのギャンブルを意思決定問題の例題としてやってきた。
私は一つのことを、寝食を忘れて極限まで追求するのが好きなので、それぞれ私なりに本気で取り組んできたし、その知見を共有することは本当に勝ちたいと思ってるあなたにとって価値があることだと思う。
一般の読者に向けて分かりやすく書くつもりなので、多少説明や例示を極端にするかもしれないけど、各分野のガチ勢の方がいたらご勘弁。
一本目は確率の認知の話。
これは私の意見ではなく、認知心理学的な分野でどっかから聞きかじった話だけど、人間は確率とランダムネスが本質的に理解出来ていないらしい。
自身の経験と観察から、この話にはとても納得出来る。
確率に対する理解が、人類の進化の過程で生存に有利に働かなかったってことなんだろうな。
サイコロを振ると6分の1の確率で1の目が出る。
これは6回振れば必ず1回1の目が出ることを意味しない。
それって一体どういうことなんだろうな。
たしかに、数学の歴史を紐解いても、ピラミッドが建設された頃から発達していた幾何学とかに比べると、確率という概念の歴史は不自然なほど浅い。
確率論の発展はせいぜい16世紀からの話で、それまで賽の目は神が決めるものとされていた。
歴史上人類がなんらかの敵と相対し、今まさに闘争せんとするとき、勝利の確率などはどうでも良かったんだと思う。
勝つか負けるか、白か黒かが重要なのであり、灰色の濃淡は参考にならない。
「今後30年のうちに巨大地震が発生する確率はp%」なんかも個人的にはどうでも良い。
パチンコで「この次300回転以内に当たる確率が65%」くらい意味のない言及だ。
実際、大当たり確率1/300のパチンコの台は、完全確率である限り、任意の回転数から300回転以内に当たる確率はそれくらいだ。
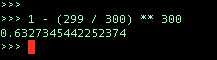
それは正しいんだろうけど、前提であって、未来の行動の指針にならないんだよな。
多くの人にとって重要なのは、当たるか当たらないか、それだけだ。
だから人は、単なる確率事象に時に超自然的な法則を見出そうとする。
神の意思とか、運命とか、あるいは験担ぎや縁起、ジンクス、オカルト、流れなんかもその類だろう。
パチンコの遠隔や、競馬の八百長的な陰謀論が常に一定の支持を受けるのも超自然的ではないにせよ、同じことが由来だと思う。
人は理解が簡単な、1対1で対応した因果関係を求めがちだ。
ギャンブルは(というかこの世界の大凡全てのことが)確率事象を扱うし、それが正しく理解できないことが、ギャンブルの難しさの主因になっている。
大げさに言えば、ギャンブルで勝利するということは、人類の進化の歴史に対する挑戦だ。
良い結果を出すために、まず確率事象に対して自分の認知がどう歪み得るか、を理解するのは有用だと思う。
自分の確率に対する直感が、ときに事実と異なり得るということを知っているのといないのとでは大違いだ。
目の錯覚のようなもので、知ったところで防ぎようがない。
だからこそパイロットは飛行訓練の前に、あらゆる目の錯覚の勉強をする。
昔アメリカで大論争を巻き起こしたモンティ・ホール問題という問題がある。
有名な問題であるし、以前私がツイッターで呟いたこともあるので、ご存知の方も多いだろう。
ルールはこうだ。
あなたはテレビのクイズ番組の出演者で、豪華商品を手に入れるチャンスを与えられた。
目の前には大きな扉が3つあり、そのうちの2つの扉の向こう側には”はずれ”を意味するヤギがいる。
当たりの扉の向こう側には高級車があり、あなたは3つの扉から一つを選ぶ。高級車の扉を選ぶことが出来れば、あなたは晴れてその車を手に入れることが出来る。
選ぶ扉はあなたの直感に頼るほかなく、ヒントは最初は一切ない。車の的中確率は1/3だ。あなたが一つの扉を選び、それを宣言したところ、車の在処を知っている司会者が、選ばれていない二つの扉のうち一つを開け、その向こうにヤギがいることを確認する。(この時、司会者は必ずヤギの扉を開ける)
そして、あなたに心変わりをする最後のチャンスを与える。
「あなたは今なら、残されている最後の一つの扉に変えることも出来ます。
どうしますか。」
あなたが取り得る最善手(車を当てる期待値を最大にする選択)は、開く扉を変えることだろうか、変えないことだろうか。
あるいは、変えても変えなくても、高級車に乗って家に帰れる確率は変わらないだろうか。
広告の下に正解を書いたので、それを見る前に回答を出して欲しい。
正解は、扉を変えた方が、高級車を持って帰れる確率が2倍になる。
ここでは詳しい解説は省略するので、納得のいかない方は「モンティ・ホール問題」でググって欲しい。
よくある誤答は「変えても変えなくても的中確率は変わらない」だけど、間違えたとしても恥ずべきことではない。
アメリカの多くの数学者たちも間違えたからだ。
目の錯覚のような問題で、こういう問題を深く考え、確率に対する認知の歪みを自覚することがギャンブルに勝利する第一歩だ。
私は、競馬における競走馬の着順は確率事象だと強く信じている。
馬の着順は確率変数であり、サイコロを同じように二回振っても異なる目が出るように、同じレースを二回やったら二つの結果が異なる結果が出ると思う。
一方で、馬券師達の殆どはレースに対して、決定論的な価値観を持っているように思う。
「競馬の予想が当たる」みたいな言葉が一般に広く受け入れられているのがその証左だ。
私の立場だと、馬券は当たるが、予想は当たるとか当たらないとかではないと思う。
それは、サイコロで次の目が何か予想しているようなものに見える。当たることもあるだろう。それは確率事象だ。
これはどちらが正しいかという話ではない。たしかめようもないからな。
ただ、決定論的な競馬観を採用すると個人的に困ったことが一つある。
自分がそのギャンブルで、最善手を取れたかどうかが、馬券の的中によってのみ評価されることになってしまう。
例えばパチンコやパチスロは、自分が最善手を取れたかどうかが判断しやすい。
パチンコでボーダー以上回る台、パチスロで6確出た台に対する勝利への最善手は、可能な限り金をブチ込むことである。
私の目的は最善手を取ることであり、目標は最善手を取り続けることであり、収支はその副産物に過ぎない。
6確出た台で10万負けても私は高らかに勝利を宣言するし、千円で8回しか回らないパチンコ台追って結果10万勝っても猛省する。
別の例を挙げると、カジノのブラックジャックは、確率的な最善判断の答えは出ている。
ベーシックストラテジーとかでググって、それを暗記するだけで最善手が取れる。
尤も、最善手を取っても期待値は1を超えないので、カジノのブラックジャックに対するメタ最善手は、ブラックジャックをしないということになるんだけど。
ラスベガスをぶっつぶせはまた別のお話。
更に別の例を挙げると、麻雀やテキサスホールデムなどの対人ギャンブルは最善手判断が少し難しい。
勿論麻雀における最速テンパイへの牌効率的な最善手はあるだろうが、時と場合、特に相対してる相手によって最善手が変わりうる。
チョキを出す相手にはグーを出すのが最善手だが、パーを出す相手にはその限りではない、みたいな話だ。
さて、話を戻すと、競馬はその最善判断の曖昧さから、どうしても”勝てば官軍”的な価値観になりがちだ。
勿論、長期的に回収率がプラスになっていれば、自分の競馬予想の手法は良い、というように逆算して自信を深めることも出来ると思う。
じゃあ、”長期的”とは一体どれくらい?というと、ここも確率や統計学の認識の曖昧さから適当な意見が蔓延っているし、恣意的に決定されることが多いと思う。
(この辺についても、一応自分なりの解は出ているのでいずれ書きたい)
ギャンブルでは、ベストを尽くして負けてしまうことなんて日常茶飯事だ。
だからこそ、収支ではなく、自分の意思決定のクオリティという観点から、自分のギャンブルを評価しなければいけない。
まとめ
- 人間は確率が正しく認識できない
- だから目の前で実現した一つの結果を過大評価しがち
- よくない